Article Peer-Reviewed
Dynamic Parameter Identification of a Bicycle Using Sliding Mode Observer and Particle Swarm Optimization
1
Laboratoire Perceptions, Interactions, Comportements Simulations des usagers de la route et de la rue (PICS-L), Components and Systems Department (COSYS), Gustave Eiffel University, Champs sur Marne 77420, France
2
Laboratoire Images, Signaux et Systèmes Intelligents, Université Paris-Est Créteil, France
*
For correspondence.
Academic Editor:
Received: 7 October 2024 Accepted: 11 July 2025 Published: 12 September 2025
Abstract
The aim of the present work is to identify the unknown dynamic parameters of a bicycle using a sliding mode observer and Particle Swarm Optimization (PSO) approaches. The estimation of bicycle dynamics requires a good knowledge of dynamic parameters such as damping coefficient, spring stiffness, and unsprung masses, among others. In this paper, suspension stiffness and damping coefficient have been identified using the Least Squares Method and compared with those obtained using the PSO technique. Real-time tests have been carried out on an instrumented bicycle equipped with various sensors to measure its dynamics. The measures coming from these sensors have been considered to validate the estimation tools. However, only the vertical wheel displacement measurements have been used to perform the observer. Experimental results are presented and discussed to demonstrate the quality of the proposed approach.
Figures in this Article
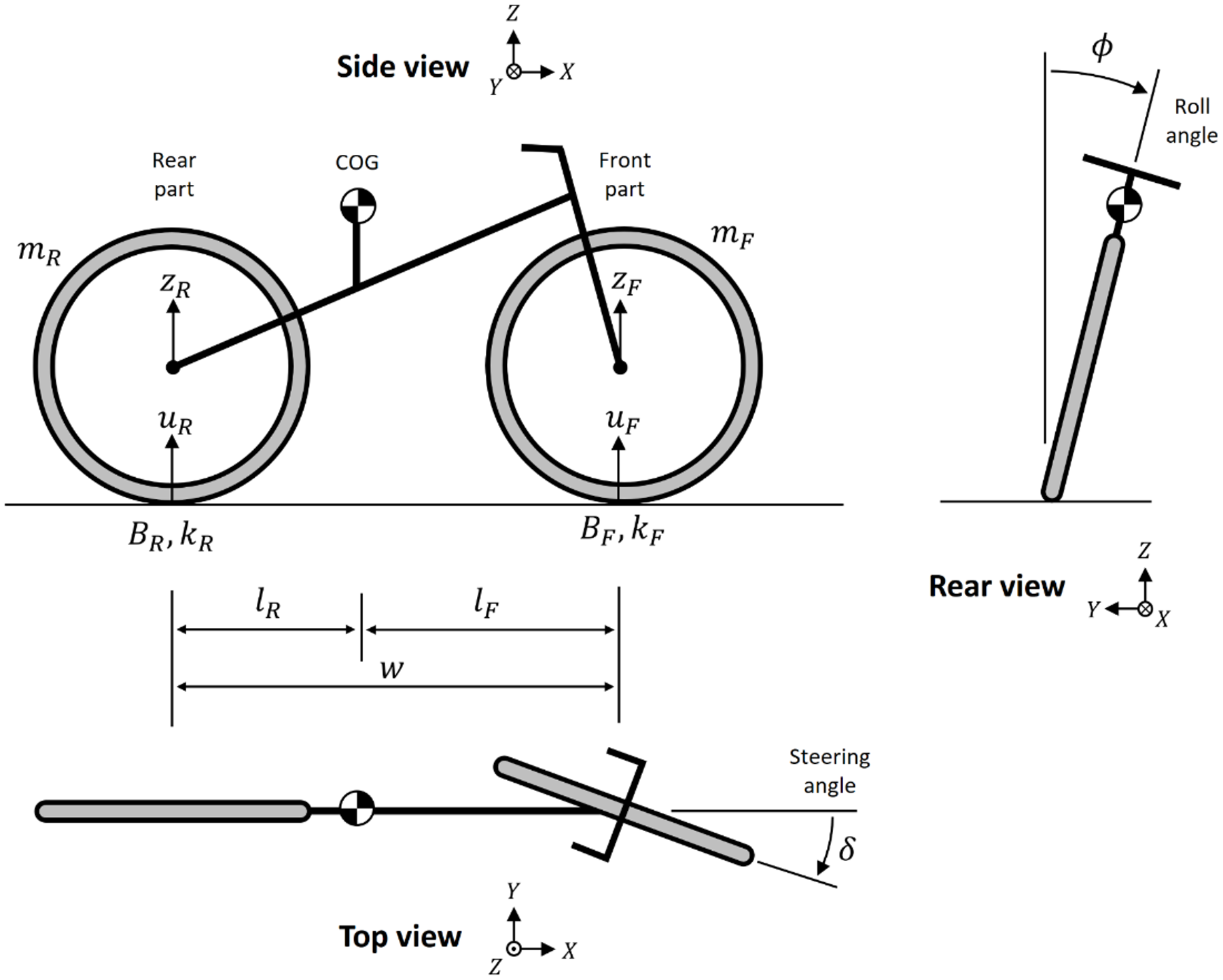 Figure 1
Figure 1
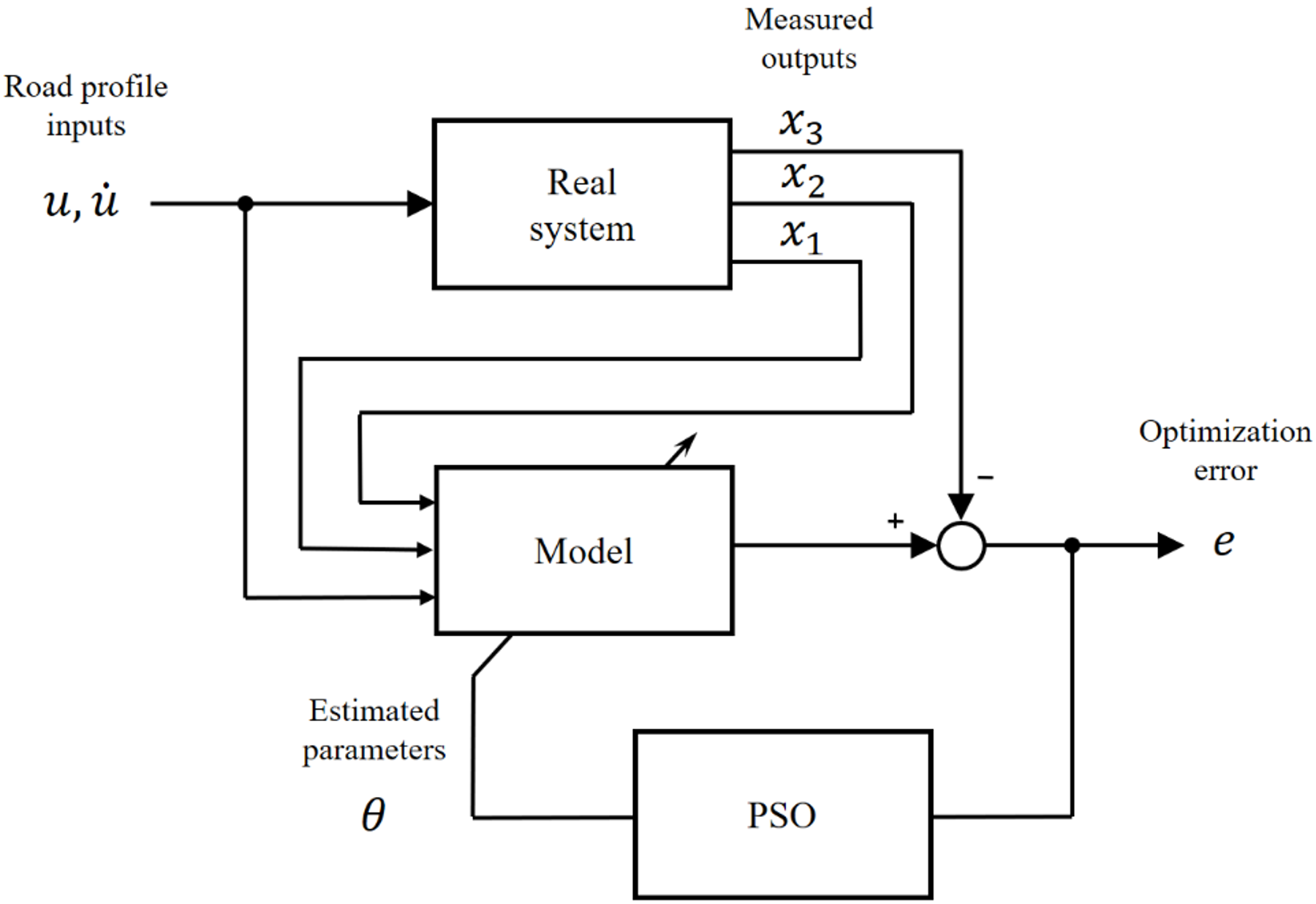 Figure 2
Figure 2
 Figure 3
Figure 3
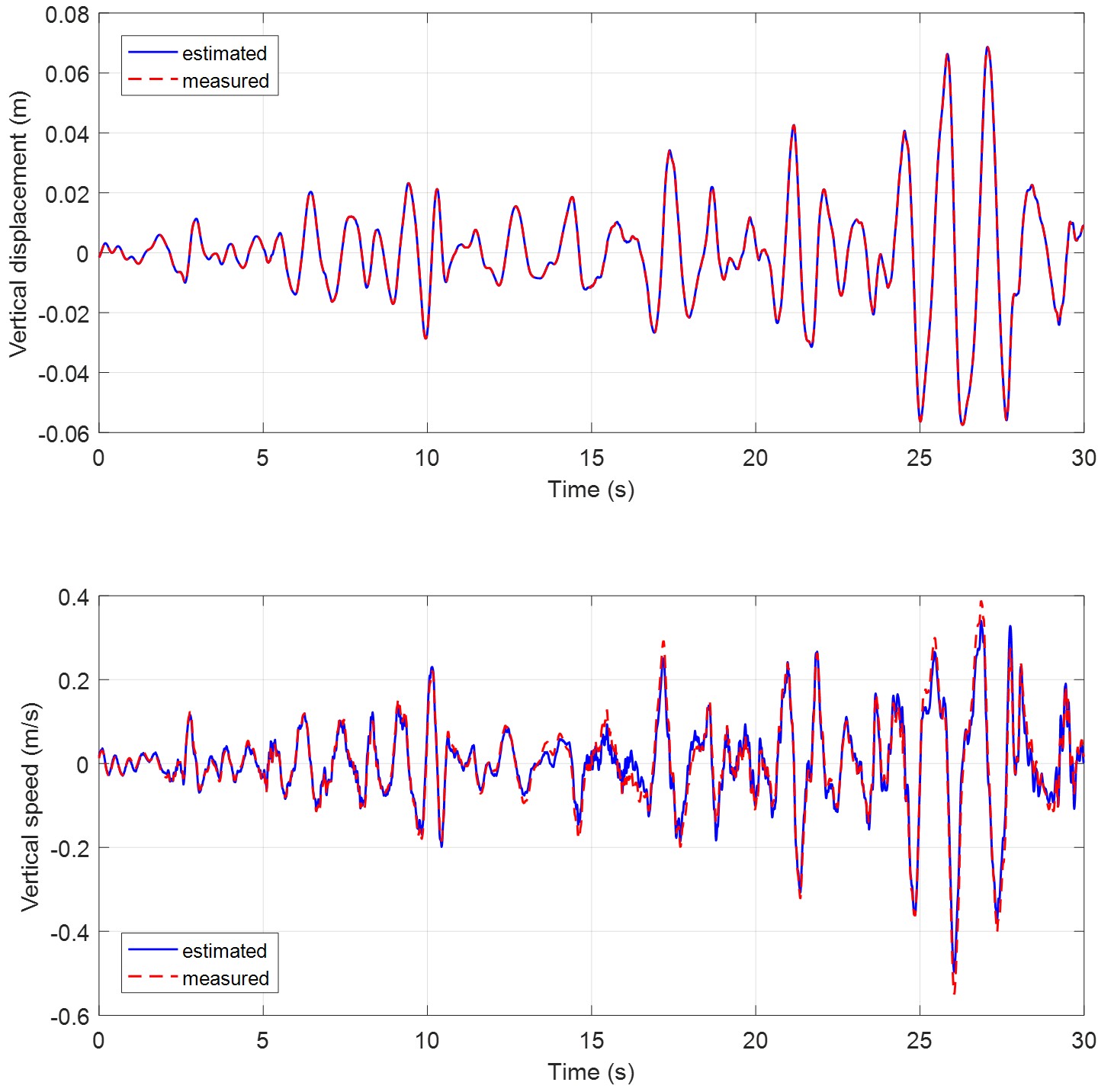 Figure 4
Figure 4
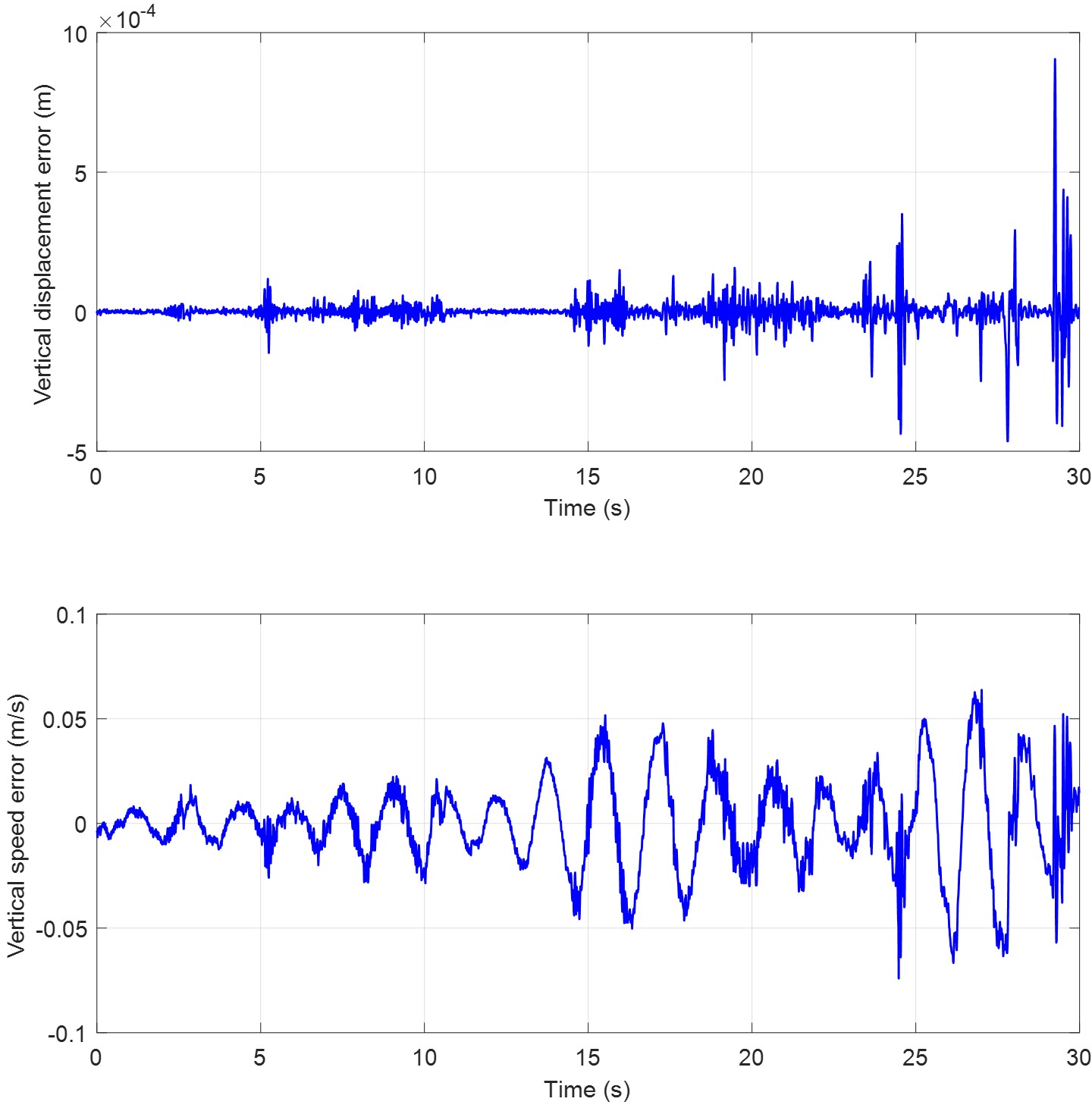 Figure 5
Figure 5
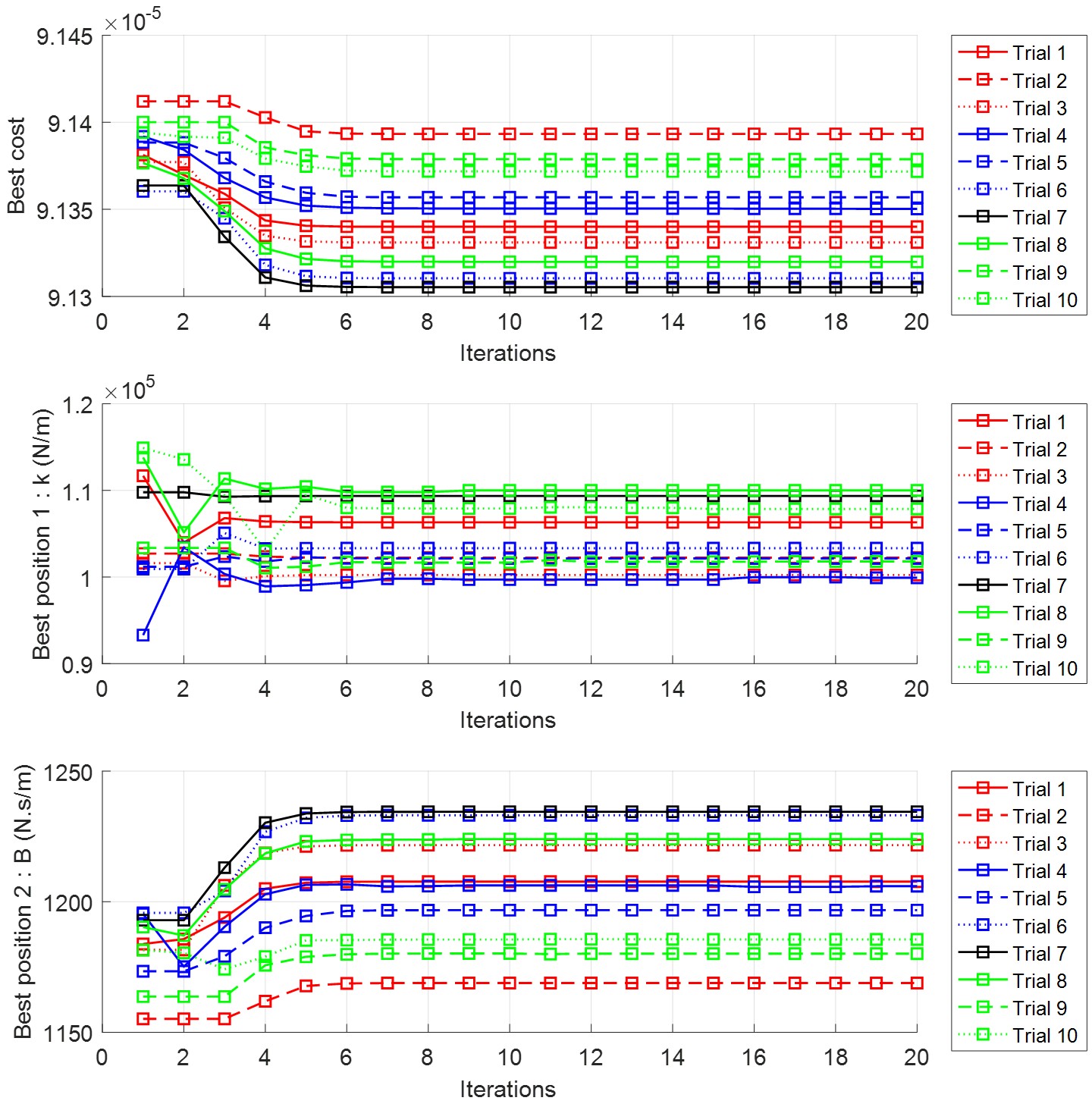 Figure 6
Figure 6
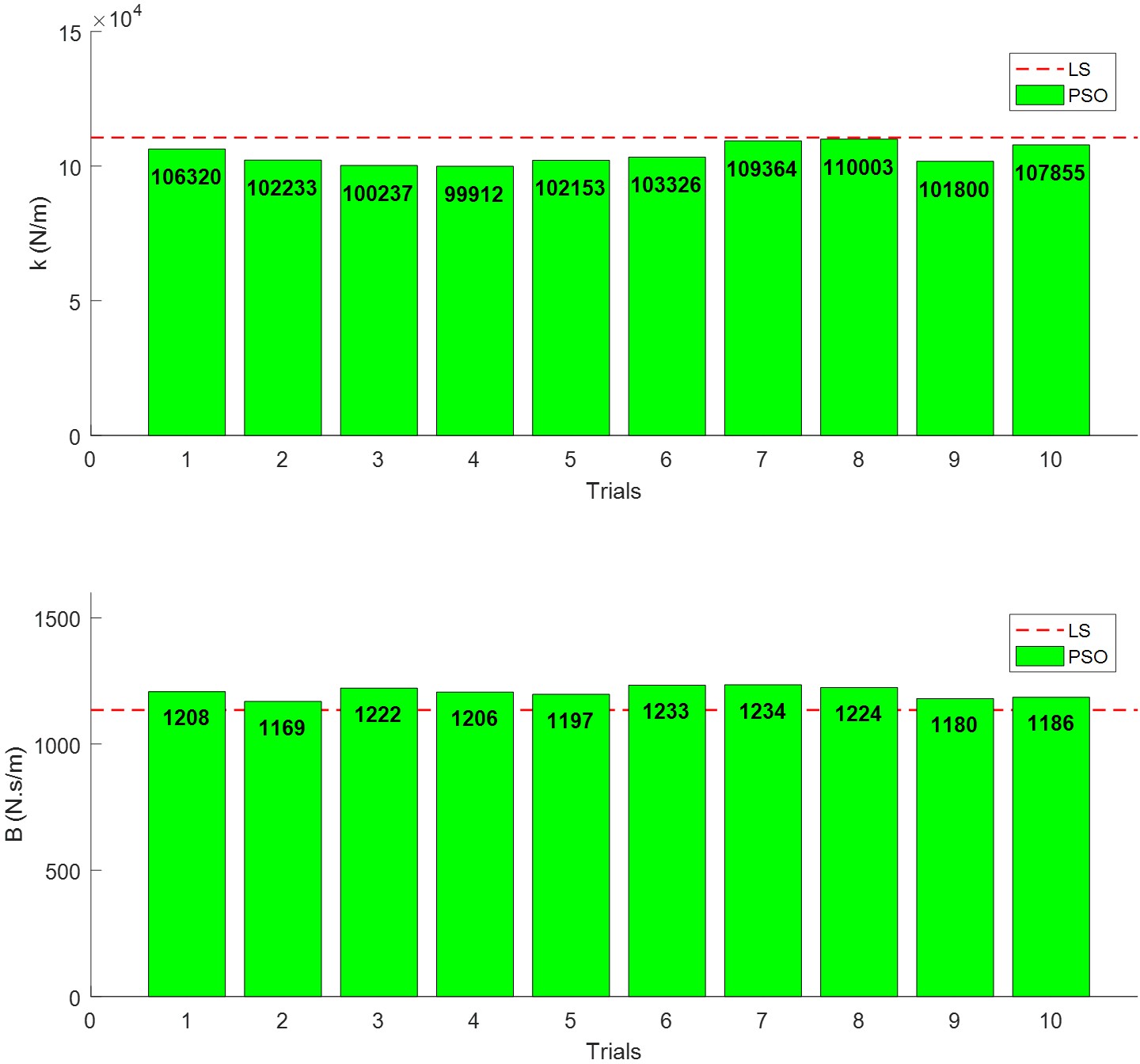 Figure 7
Figure 7
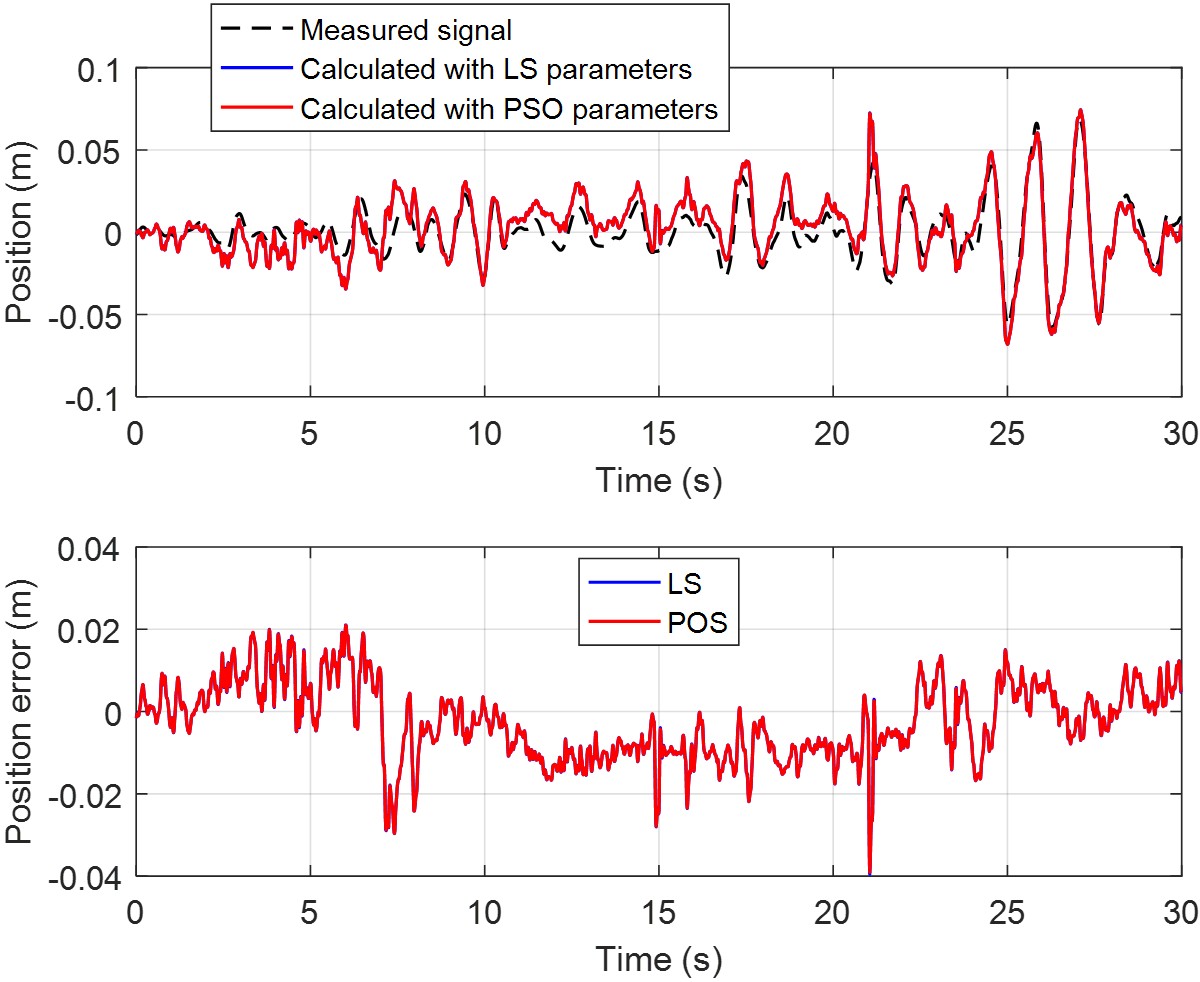 Figure 8
Figure 8
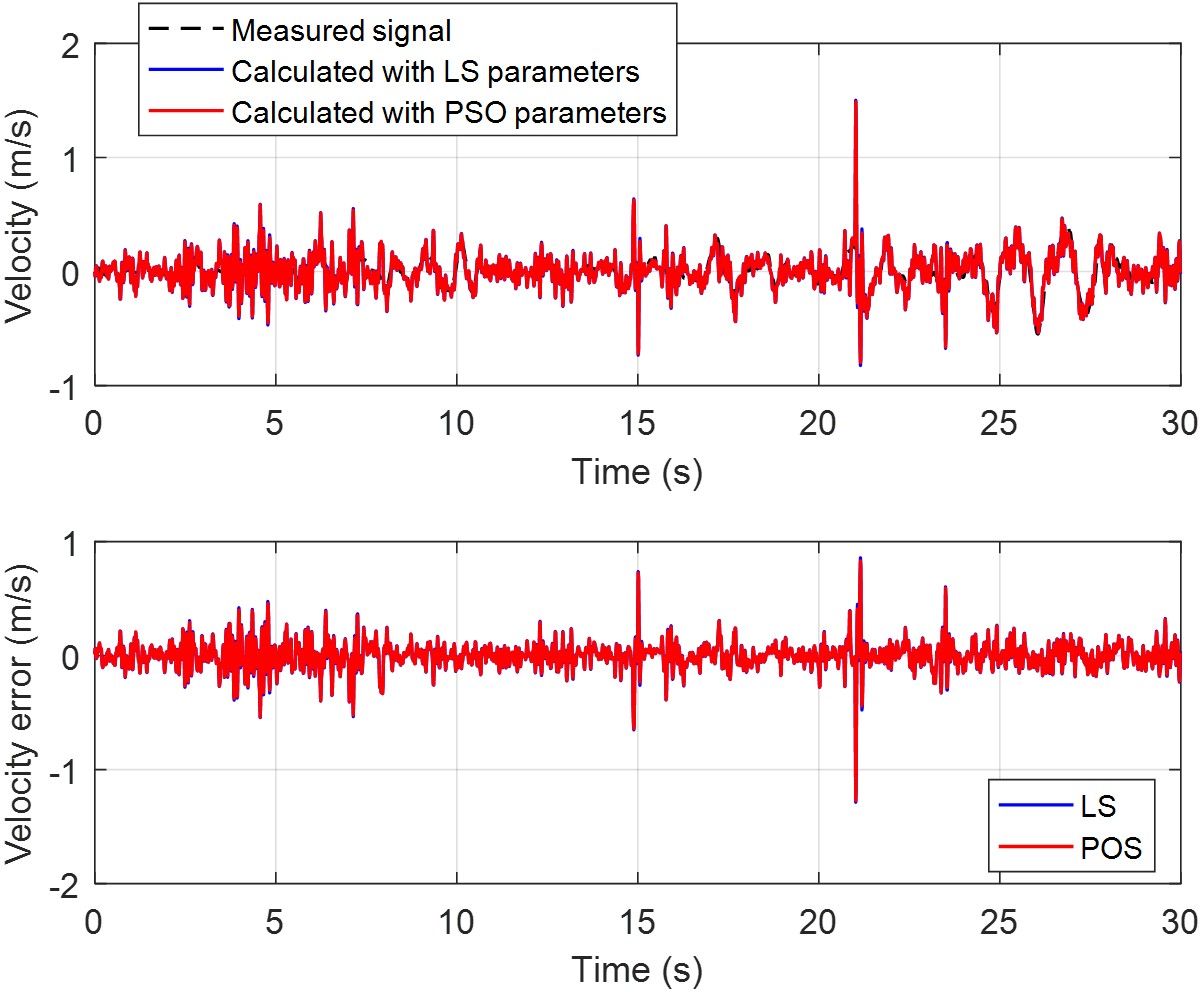 Figure 9
Figure 9
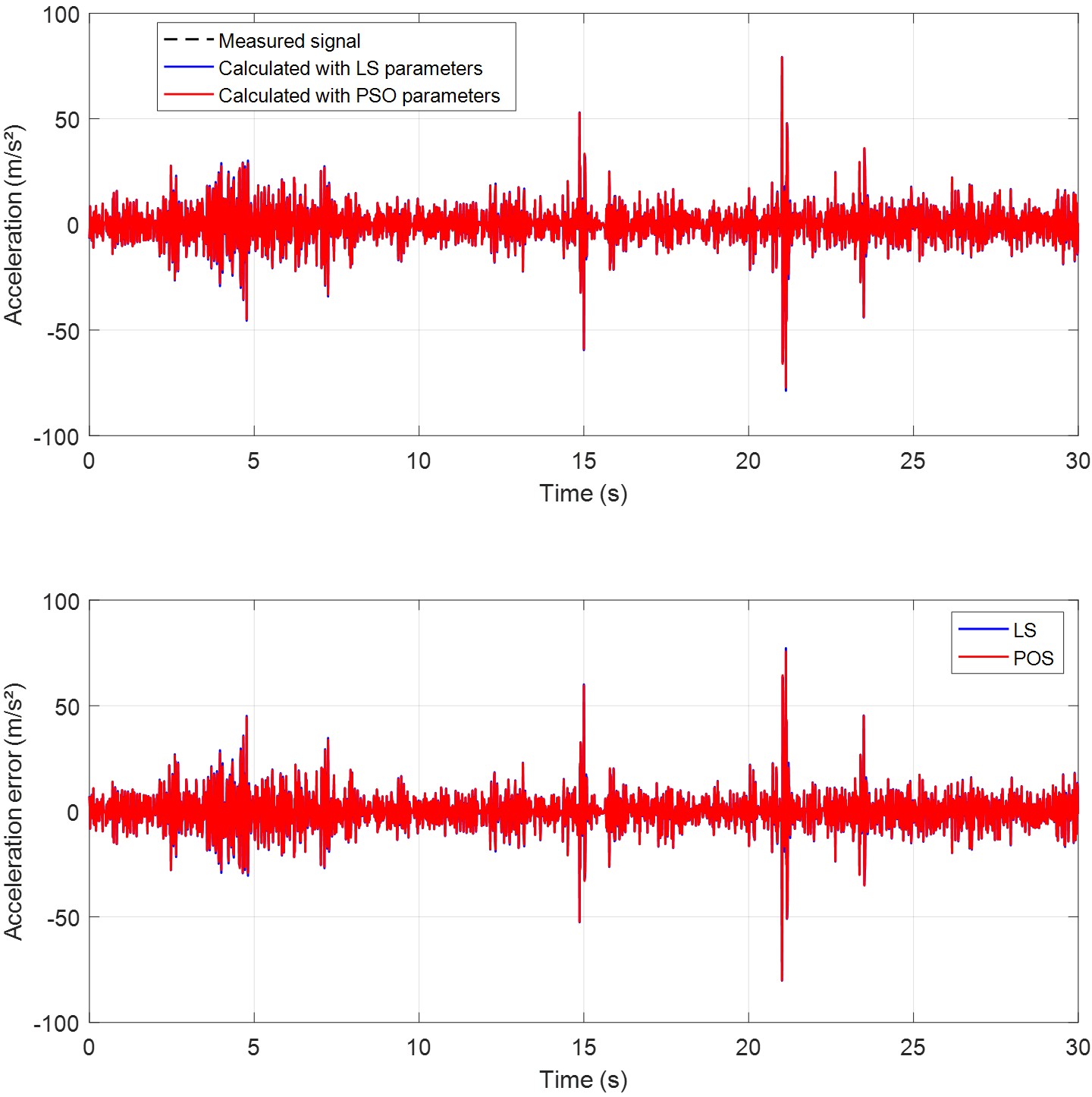 Figure 10
Figure 10
Keywords
Copyright © 2025
Imine et al. This article is distributed under the terms of the Creative Commons Attribution License (CC BY 4.0), which permits unrestricted use and distribution provided that the original work is properly cited.
Funding
This work is funded by Marie Skłodowska-Curie actions (H2020 MGA MSCA-ITN) within the SAFERUP project under grant agreement number 765057.
Cite this Article
Imine, H., Madani, T., & Shoman, M. (2025). Dynamic Parameter Identification of a Bicycle Using Sliding Mode Observer and Particle Swarm Optimization. Highlights of Vehicles, 3(2), 15–29. https://doi.org/10.54175/hveh3020002
References
1.
Shoman, M., Simone, A., & Vignali, V. (2018). Looking behavior to vertical road signs on rural roads. MOJ Civil Engineering, 4(2), 75–79.
2.
Billot-Grasset, A., Amoros, E., & Hours, M. (2016). How cyclist behavior affects bicycle accident configurations? Transportation Research Part F: Traffic Psychology and Behaviour, 41, 261–276.
3.
Shoman, M., & Imine, H. (27–30 April 2020). Modeling and simulation of bicycle dynamics. The 8th Transport Research Arena TRA 2020, Helsinki, Finland.
4.
Shoman, M., & Imine, H. (18–22 October 2020). Subjective validity of bicycle simulators. The Ninth International Conference on Advances in Vehicular Systems, Technologies and Applications, Porto, Portugal.
5.
Shoman, M., & Imine, H. (2021). Bicycle Simulator Improvement and Validation. IEEE Access, 9, 55063–55076. https://doi.org/10.1109/ACCESS.2021.3071214
6.
Owczarkowski, A., Horla, D., Kozierski, P., & Sadalla, T. (29 August–1 September 2016). Dynamic modeling and simulation of a bicycle stabilized by LQR control. The 21st International Conference on Methods and Models in Automation and Robotics (MMAR), Miedzyzdroje, Poland. https://doi.org/10.1109/MMAR.2016.7575258
7.
He, Q., Fan, X., & Ma, D. (2005). Full bicycle dynamic model for interactive bicycle simulator. Journal of Computing and Information Science in Engineering, 5(4), 373–380. https://doi.org/10.1115/1.2121749
8.
Whipple, F. J. (1899). The stability of the motion of a bicycle. The Quarterly Journal of Pure and Applied Mathematics, 30, 312–321.
9.
Fridman, L., Levant, A., & Davila, J. (13–15 December 2006). High-Order Sliding-Mode Observation and Identification for Linear Systems with Unknown Inputs. The 45th IEEE Conference on Decision and Control, San Diego, CA, USA. https://doi.org/10.1109/CDC.2006.377385
10.
Imine, H., Benallegue, A., Madani, T., & Srairi, S. (2014). Rollover risk prediction of heavy vehicle using high order sliding mode observer. IEEE Transactions on Vehicular Technology, 63(6), 2533–2543. https://doi.org/10.1109/TVT.2013.2292998
11.
Baldini, A., Ciabattoni, L., Felicetti, R., Ferracuti, F., Freddi, A., Monteriù, A., et al. (2017). Particle swarm optimization based sliding mode control design: Application to a quadrotor vehicle. In S. Vaidyanathan & C. H. Lien (Eds.), Applications of Sliding Mode Control in Science and Engineering (pp. 143–169). Springer, Cham. https://doi.org/10.1007/978-3-319-55598-0_7
12.
Shetty, S., Kareem, A., & Aithal, G. (2022). Integration of Particle Swarm Optimization and Sliding Mode Control: A Comprehensive Review. In International Conference on VLSI, Signal Processing, Power Electronics, IoT, Communication and Embedded Systems (pp. 205–213). Springer, Singapore. https://doi.org/10.1007/978-981-99-4444-6_1
13.
Kennedy, J., & Eberhart, R. C. (1995). Particle swarm optimization. In Proceedings of the IEEE International Conference on Neural Networks (pp. 1942–1948). IEEE. https://doi.org/10.1109/ICNN.1995.488968
14.
Kennedy, J., Eberhart, R. C., & Shi, Y. Y. (2001). Swarm Intelligence, The Morgan Kaufmann Series in Artificial Intelligence. Morgan Kaufmann.
15.
Shi, Y., & Eberhart, R. C. (1998). A modified particle swarm optimizer. In Proceedings of the Conference on Evolutionary Computation (pp. 69–73). IEEE. https://doi.org/10.1109/ICEC.1998.699146
16.
Zhu, J., Zhao, J., & Li, X. (2008). A new adaptive particle swarm optimization algorithm. In 2008 International Workshop on Modelling, Simulation and Optimization (pp. 456–458). IEEE. https://doi.org/10.1109/WMSO.2008.115
17.
Deng, X. (11–14 December 2009). System identification based on particle swarm optimization algorithm. The 2009 International Conference on Computational Intelligence and Security, Beijing, China. https://doi.org/10.1109/CIS.2009.167
18.
Kiencke, U., & Nielsen, L. (2000). Automotive control systems: For engine, driveline, and vehicle. Measurement Science and Technology, 11(12), 1828. https://doi.org/10.1088/0957-0233/11/12/708
19.
Damon, P.-M. (2018). Estimation pour le développement de systèmes d’aide à la conduite des véhicules à deux-roues motorisées (in French) [PhD Thesis]. Université d’Evry-Val-d’Essonne.
20.
Levant, A. (2003). High-order sliding modes: differentiation and output-feedback control. International Journal of Control, 76(9–10), 924–941. https://doi.org/10.1080/0020717031000099029
21.
Hedrick, J. K., Rajamani, R., & Yi, K. (1994). Observer Design for Electronic Suspension Applications. Vehicle System Dynamics, 23(6), 413–440. https://doi.org/10.1080/00423119408969068
22.
Soderstrom, T., & Stoica, P. (1989). System Identification. Prentice Hall International.
23.
Floret-Pontet, F., & Lamnabhi-Lagarrigue, F. (2001). Parameter Identification Methodology Using Sliding Mode Observers. International Journal of Control, 74(18), 1743–1753. https://doi.org/10.1080/00207170110089761
24.
Poli, R., Kennedy, J., & Blackwell, T. (2007). Particle swarm optimization. Swarm Intelligence, 1, 33–57. https://doi.org/10.1007/s11721-007-0002-0
25.
Ratnaweera, A., Halgamuge, S. K., & Watson, H. C. (2004). Self-organizing hierarchical particle swarm optimizer with time-varying acceleration coefficient. IEEE Transactions on Evolutionary Computation, 8, 240–255. https://doi.org/10.1109/TEVC.2004.826071
26.
World Health Organization. (2018). Global Status Report on Road Safety 2018.
27.
Observatoire national interministériel de la sécurité routière. (2017). La Sécurité Routière en France Bilan de l’accidentalité de l’année (in French).
Metrics
Loading...
Journal Menu
Journal Contact
Highlights of Vehicles
Editorial Office
Highlights of Science
Avenida Madrid, 189-195, 3-3
08014 Barcelona, Spain
08014 Barcelona, Spain
Mr.
Jene Zhang
Managing Editor